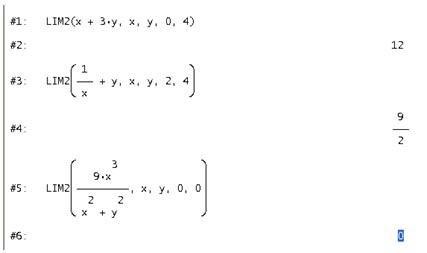Límites en Derive                                                         
      Además de las operaciones que se comentan anteriormente podemos calcular límites, derivadas, derivadas parciales e integrales en Derive. En primer lugar veremos cómo resolver límites con Derive.
      En Derive podemos hallar tanto límites como límites laterales. Existen diferentes formas de introducir un límite para su posterior cálculo. La primera forma de introducir un límite sería, después de escribir en la línea de autor la función o expresión de la que queremos calcular el límite y tenerla en la ventana de trabajo, seleccionar en el menú Calculus -> Limit, o bien CTRL+SHIFT+L. En la barra de herramientas disponemos también de un botón  que nos permite calcular límites. Con esto nos aparecerá una ventana en la que deberemos seleccionar la variable respecto de la cual calculamos el límite, hacia donde tiende el límite y si queremos calcular el límite lateral por la derecha, por la izquierda o ambos. Una vez configurado todo esto, si hacemos click sobre “Simplify”, nos aparecerá el límite en el área de trabajo y la solución de dicho límite. Podemos ver una ejemplo en la imagen siguiente.

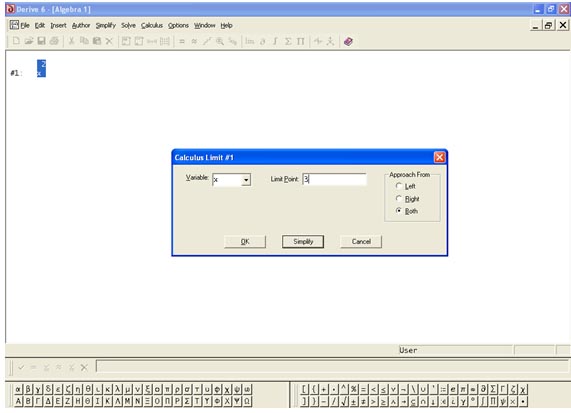
      En el ejemplo de la imagen vamos a calcular el límite de la función 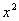 cuando 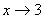. Vemos que en la parte derecha de la ventana de límite podemos seleccionar la manera en que nos acercamos al punto límite: izquierda, derecha o ambas. En el primer campo de la ventana “Variable” debemos seleccionar la variable que tiende a dicho punto y en el segundo campo, el valor al que tiende. Una vez configurados todos estos campos, podemos seleccionar bien  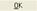o bien . Si seleccionamos la primera de estas opciones, simplemente nos aparecerá la expresión en la ventana de autor, sin resolver. Para esto, deberemos pulsar sobre  y nos aparecerá tanto la expresión como la solución del límite, tal y como observamos en la imagen de abajo.

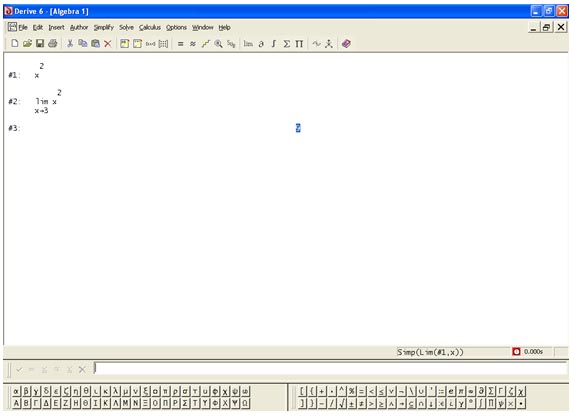
      Otra forma de escribir y calcular un límite es con la función predeterminada que nos ofrece Derive. Para ello, tenemos:

      LIM(u,x,a): esta función calcula el límite de la función ‘u’ cuando la variable ‘x’ tiende a ‘a’.

      En caso de que queramos calcular el límite lateral derecho o el límite lateral izquierdo deberemos de introducir un cuarto argumento. Para esto, en caso de querer calcular el límite por la derecha de una determinada expresión, introduciremos como cuarto argumento un número positivo: LIM(u,x,a,1). En caso contrario, introduciremos un número negativo: lim(u,x,a,-1). Podemos ver un ejemplo de cada uno de esto casos en la imagen siguiente.

      Derive también nos da la oportunidad de calcular límites de dos variables, es decir, límites en los que las variables ‘x’ e ‘y’ tienden a ‘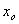’ e ‘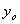’. Para ello, disponemos de un archivo de utilidad (Utility file) en el que viene definida la función LIM2 para este tipo de ejercicios.
      La función LIM2 tiene como argumentos  la expresión de la que queremos calcular el límite, las dos variables y los puntos a los que tienden ambas. Con esto tenemos LIM2(u,x,y,x0,y0). Podemos ver un ejemplo en la siguiente ilustración.

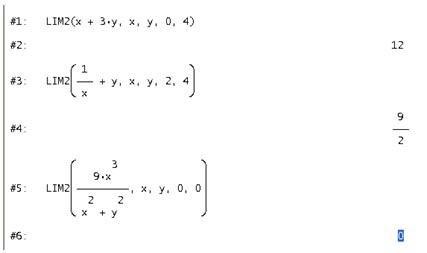
      No obstante, para generalizar y hacer un límite con ‘n’ variables podemos hacer uso de la función LIM explicada anteriormente. Para ello lo que debemos hacer es lo siguiente. Debemos pasarle como expresión la que queramos, con tantas variables como tengamos. Como segundo argumento, le debemos pasar un vector compuesto por las variables que forman la expresión. Y, finalmente, deberemos meterle como tercer argumento un vector en el cual los elementos del mismo son los valores a los que deben tender cada una de las variables que forman la expresión introducida. Veamos un ejemplo.